REFERENTE (Estándar,
propósito o DBA):
1. Reconoce que la gráfica de y = mx + b es una línea recta.
2. Encuentra la ecuación de la recta (y = mx + b) que pasa por dos puntos dados y comprende el
significado gráfico de m y b.
3. Comprende que para calcular la pendiente (m) de una recta se puede
utilizar dos puntos cualesquiera
sobre la recta.
4. Comprende que cualquier pareja de puntos (x, y) que satisfaga la relación y = mx + b corresponde a
un punto sobre la línea, y cualquier punto (x, y) sobre la línea satisface la relación y = mx + b.
En esta clase
hablaremos especialmente del tema de funciones lineales, prestando principal
atención a:
- Reconocimiento y construcción
del plano cartesiano
- Identificación y desarrollo
de la ecuación y = mx + b
- Tabulación y graficación de
funciones
- Desarrollo de problemas de
aplicación.
Empecemos hablando del plano cartesiano:
“El nombre del plano cartesiano se debe al filósofo y matemático francés René Descartes, quien fue el creador de la geometría analítica y el primero en utilizar este sistema de coordenadas.
Se conoce como plano cartesiano, coordenadas
cartesianas o sistema cartesiano a dos rectas numéricas perpendiculares, una
horizontal y otra vertical, que se cortan en un punto llamado origen o punto
cero.
La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual está representada por el sistema de coordenadas.
El plano cartesiano sirve también para analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la línea, la circunferencia y la elipse, las cuales forman parte de la geometría analítica”.
Plano cartesiano. Recuperado el 5 de junio de 2020 en:
Los elementos del plano cartesiano son:
Eje x o también llamado eje de las abscisas. Es la recta horizontal en el plano.
Eje y o también llamado eje de la ordenada. Es la línea vertical en el plano
Punto de origen. Es el punto donde se cortan los dos ejes x e y formando la perpendicular.
Cuadrantes I, II, III, IV
Signos de los cuadrantes: Cuadrante I es positivo, cuadrante II es negativo, Cuadrante III es positivo,
Cuadrante IV es negativo. (Los cuadrantes se nombran en dirección contraria al giro de las manecillas del reloj
Coordenadas: Las coordenadas son los números que nos dan la ubicación del punto en el plano. Las coordenadas se forman asignando un determinado valor al eje “x” y otro valor al eje “y”. Esto se representa de la siguiente manera:
P (x, y), donde:
P = punto en el plano;
x = eje de la abscisa (horizontal);
y = eje de la ordenada (vertical).
Veamos en el vídeo los elementos del plano cartesiano:
En
el plano se observan las parejas ordenadas P(x,y):
a. P(2,3) en el cuadrante I
b. P(-3,1) en el cuadrante II
c. P(-3,-3) en el cuadrante III
d. P(3,-2) en el cuadrante IV
Veamos el vídeo sobre plano cartesiano:
Practica lo visto hasta el momento: Resuélvelo en tu cuaderno de teoría.
1. Dibuja un plano cartesiano y señala en él todos sus elementos
2. Dibuja otro plano cartesiano y ubica en él las siguientes coordenadas o parejas ordenas (x,y)
a. P(2,6)
b. P(- 7,4)
c. P(-5,-3)
d. P(6,-8)
Funciones en un plano cartesiano.
Una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:
F(x) = mx + b
Donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica mentonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b= 0 de la forma:
Y = mx
mientras que llaman función afín a la que tiene la forma:
F(x) = mx + b
En una función lineal, el coeficiente del término en x lo llamamos pendiente de la línea recta y la representamos por la letra m.
Cuando se trata de una función lineal (es decir, que no tiene término independiente) la línea recta pasa por el punto de origen.
Cuando es una función afin (es decir, que tiene término independiente), la gráfica corta al eje y según ese término independiente.
Veamos los conceptos y gráficas en el vídeo:
Una función representada como: f(x)=y es una operación para obtener de un variable independiente (dominio) las variables dependientes (contra dominio). Por ejemplo: f(x)=5x
Veamos el vídeo de apoyo. Tabulación y graficación:
|
Función f(x) = 5x |
Dominio |
Contradominio |
P(x,y) |
|
F(1) = 5x |
1 |
2 |
(1,2) |
|
F(2) = 5x |
2 |
10 |
(2,10) |
|
F(3) = 5x |
3 |
15 |
(3,15) |
|
F(4) = 5x |
4 |
20 |
(4,20 |
La
relación del dominio y el contra dominio es biunívoca, lo que significa que
tiene solo dos puntos correctos.
Para encontrar la función en un plano cartesiano se debe primero tabular, o sea, ordenar los puntos en una tabla las parejas encontradas para posicionarlas o ubicarlas después en el plano cartesiano.
Es importante que la expresión y = mx +b, también puede expresarse de la forma f(x) = mx + b
Ejemplo de tabulación y graficación.
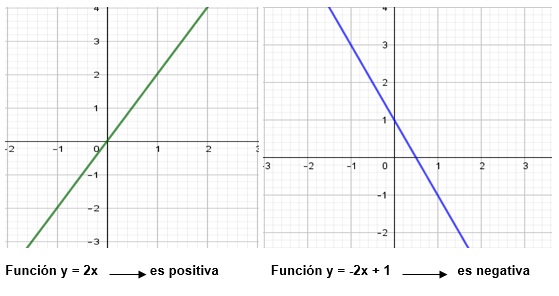
La gráfica de una función lineal (y= mx + b) es una línea recta.
Una función es positiva cuando el coeficiente en el término en x es positiva y es negativa cuando el coeficiente es negativo.
En la gráfica podemos determinar si la función es positiva cuando la línea recta sube o busca cuadrantes positivos y es negativa cuando la línea recta baja o busca cuadrantes negativos.
Tabule y grafique f(x) = 2x
· Primero hacemos una tabla y asignamos valores a la variable x. Se recomienda valores cercanos a cero.
·
Luego
se resuelve la operación resultante.
Veamos: f(x) = 2x
|
X |
F(1) |
F(2) |
F(3) |
F(4) |
|
y |
2 |
4 |
6 |
8 |
2.
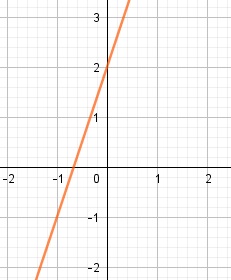
Tabule y grafique la función: y = 3x + 2
3(-2)
+ 2 = -6 + 2 = -4
3(-1)
+ 2 = -3 + 2 = -1
3(0)
+ 2 = 0 + 2 = 2
3(1)
+ 2 = 3 + 2 = 5
|
x |
y |
|
-2 |
-4 |
|
-1 |
-1 |
|
0 |
2 |
|
1 |
5 |
APLICACIONES
DE LAS FUNCIONES LINEALES.
Las funciones nos sirven para aplicar en la solución de problemas de nuestra vida real.
Veamos el vídeo con aplicaciones de las funciones lineales:
Ejemplo 1
Ejemplo 2
10. Un auto circula por una autopista recta a velocidad constante. El copiloto cuenta las farolas
que hay en la calzada:
- Cuando lleva 1 minuto, ha observado 3 farolas.
- Cuando lleva 3 minutos, ha observado 15 farolas.
- Obtener la función que proporciona el número de farolas vistas en función del tiempo sabiendo que es una ecuación lineal.
- ¿Cuántas farolas habrá visto en media hora?
- Tabule y grafique.
BIBLIOGRAFÍA:
- Los caminos del saber. Matemáticas 8. Editorial Santillana.
CIBERGRAFÍA
- Plano cartesiano. Recuperado el 5 de junio de 2020 en: https://www.significados.com/plano-cartesiano/
- Aplicaciones de las funciones lineales. Recuperado el 5 de junio de 2020 en: https://sites.google.com/site/mate1equipo5usilcpel/03-clases/10-aplicaciones-de-la-funcion-lineal
- Canal de YouTube
Lunes 11 de mayo de 2020
Vídeo 2.
Ahora continuaremos con la conceptualización. Lee muy bien y practica.
Ahora resolveremos las siguientes actividades de práctica:
_________________________________________________________________________
MARTES 17 DE MARZO DEL 2020
Clase para el clei 4
Vean los 4 vídeos que aparecen a continuación. Introducción al álgebra, lenguaje algebraico, reducción de términos semejantes sin y con paréntesis.
Los vídeos te servirán de repaso a lo visto en clase anterior.
Introducción al álgebra
Introducción al álgebra. Lenguaje algebraico
Reducción de términos semejantes con signos de agrupación
Elementos de un término
Grado de un término y grado de un polinomio
Clasificación de los polinomios.
Términos semejantes y reducción de términos semejantes
Según lo visto en clase anterior y lo visto en los vídeos resuelve la siguiente actividad
Desarrollar la actividad en el cuaderno de teoría. Enviar la solución en la plataforma de Edmodo.
Plazo hasta el día viernes 20 de marzo a las 11:59 pm. Resolver en forma individual.
Sábado 15 de febrero del 2020
Hola amigo y amiga de la jornada nocturna. Aquí encontrarás a partir de la próxima semana información de tu interés y pequeños retos para resolver y que de pasó te darán puntos positivos en la materia, que sin lugar a dudas te ayudarán en tu proceso.
Por ahora, se el primero en entregar en la primera clase de matemáticas que tengas con tu profesor, éste mismo texto copiado en una hoja de bloc. Debes hacerle portada.
Si eres el primero ganas puntos positivos.

















Gabriela Moreno Araque (Clei 4 Nocturna)
ResponderEliminarolga espinal
ResponderEliminarMateo Gonzalez Restrepo (C
ResponderEliminarlei 4 nocturna)
mateo gonzalez restrepo clei 4
ResponderEliminarSergio andres serna espinosa
ResponderEliminar