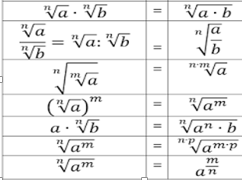Perímetros y áreas de figuras planas

Perímetros de figuras planas

Perímetros de figuras planas

Racionalización

Racionalización

Operaciones con radicales

operaciones con radicales

El juego del trueque

El juego del trueque:

Relacionando la economía con las matemáticas, este juego consiste en que cada alumno presenta el día que le corresponda su evaluación final correspondiente un pensemos o juego matemático resuelto (en hojas en blanco tamaño carta, con portada y el juego  resuelto). Deberá entregárselo al docente que está aplicando la prueba. Quien quiera jugar a este juego, deberá escoger 3 puntos de la evaluación que quiera cambiar (No responder).

La condición para participar es que cada estudiante lo haga saber en este blog y en los comentarios de esta misma publicación, registrando su nombre y el grado.

En Economía también es válido este juego, pero aquí cada alumno presenta en trabajo escrito tipo informe la noticia económica que tiene que ver con el incremento salarial para los empleados estatales en el año 2019. El trabajo deberá ser presentado en hojas tamaño carta con portada. Resumen y conclusión personal sobre la noticia. Si cumple con las indicaciones dadas, podrá cambiar 2 puntos de la evaluación.

Prof. Éver Chalarca Bedoya. 

Aplicaciones

Razones trigonométricas

Relaciones trigonométricas del triángulo rectángulo

Taller de repaso del segundo período

TALLER DE REPASO – GRADO 7,2

SEGUNDO PERÍODO 2019

1. Enuncie cada una de las propiedades de la multiplicación (asociativa, conmutativa, distributiva y 

    Modulativa) y de 2 ejemplos de cada una.

2. Dados los productos 2 x 1 x 4 x 8 x 7, aplique la propiedad asociativa y conmutativa.

3.  La expresión “Cualquier número entero multiplicado por 1, da como resultado el mismo número entero”, corresponde a la propiedad:

A.    Modulativa de la multiplicación

B.    Conmutativa de la multiplicación

C.    Asociativa de la multiplicación

D.    Distributiva de la multiplicación

4. Elimine los paréntesis y resuelva:

1).     – (18 – 32 + 2) + (12 + 4)

2).     (15 – 23) – (11 + 9) - 50

5.  Elimine los signos de agrupación y  halle el resultado de:

1).     {35+18- [40-15+20 (12-18)]}

2)      - {35+18- [40-15+20+ (12-18)]} - 10

 

6.  Escriba el conjunto de los números enteros  ≥ -2

7.  Escriba el conjunto de los números enteros   ≤  6

8. Escriba el conjunto de los números enteros  ≤ - 2 y ≤-  6

9. Represente en la recta numérica por separado los conjuntos numéricos de los puntos 6, 7 y 8

10. Escriba entre cada parejas de números, los signos  ,  =, según corresponda: La respuesta en la hoja de

      operaciones.

a.     – 3 _____ 5

b.    8 ______ -10

c.     6 ______ - 6

d.    15 _____ 15

e.     0 ______ - 5

f.     – 1 _____ 0

Lea y resuelva los problemas planteados:

11.  Si el papá de Leopoldo tiene una deuda de $ 1.000.000 y al cabo de 1 año la deuda se le triplicó, 

       entonces tiene que pagar:

A.    $ 3.000.000

B.    $ 6.000.000

C.    $ 5.000.000

D.    $ 1.000.000

12. La mamá de Juanita va a hacer mercado y tiene en su poder $ 200.000. Compra carne por $ 50.000, arroz y frijol por $ 45.000, aceite y panela por $ 35.000, frutas y verduras por $ 25.000 y pasajes del motorratón

      $ 4.000. Además paga una cuota de $ 35.000 en la cooperativa. ¿Cuánto dinero le queda a la mamá de

      Juanita?

 13. Un alpinista del Monte Éverest parte hacia la cima desde una base que está a 4.000 m. El primer día 

       logra ascender 800 metros, al segundo día 300 metros y al tercer día por mal tiempo tiene que retroceder 

       1.200 m. Al cuarto día sólo logra subir 100 m.  Responda.

1). ¿Cuántos metros ascendió?

2). ¿Cuántos metros descendió?

3). ¿A qué altura de la montaña se encuentra al finalizar el cuarto día?

14.  Resuelva aplicando las propiedades de las potencias:

1).  2⁴ x 2³ x  2²

2).  (( 2 )² )³

3).  ((( 2 )² )³ )⁰

4.    3² x 2² x  4²

15.  Determine el perímetro de las siguientes figuras:

Prof. Éver Chalarca Bedoya

Taller de repaso segundo período

TALLER DE REPASO – GRADO 9, 1,2

SEGUNDO PERÍODO 2019

  

1.       Resuelva las siguientes expresiones algebraicas con productos notables o casos de factorización según sea el caso:

1).  (4x – 7) (4x - 7)

2).  169m¹⁰ – 78m⁵ + 9

3).  9y⁴ – 100:

4).  25x³ + 15x² – 10x

5).  3abx² – 2y² – 2x² + 3aby²

6).  x² – 2x - 120                                                                                     

 2.  Al resolver la inecuación   – 12x + 15 ≥ - 13 – 2x, el valor de la x es:

A.    x ≥ 5

B.    x ≤ 1/5

C.    x ≥ 1/5

D.    x ≤  - 1/5

3. Expresa la solución a la inecuación anterior por intervalo y por comprensión

4. Dada la gráfica, exprese la solución por intervalo y por comprensión

5.  Dado el conjunto por comprensión:  A=  :  A= {x /x ∈R,-5≤x ≤  1}  , su representación por intervalo es:

v  Sean las gráficas:.

6. El intervalo   ] ∞, 3 ] representa la solución de:

A.    La figura 1

B.    La figura 2

C.    La figura 3

D.    La figura 4

7. El intervalo   ]5, ∞ [  representa la solución de:

A.    La figura 1

B.    La figura 2

C.    La figura 3

D.    Ninguna de las anteriores

8. Exprese la solución numérica y por comprensión de cada una de las figuras o gráficas dadas.

v  Dados los problemas, plantee una solución y resuélvalos

9.  Una camioneta pesa  875 kg. La diferencia entre el peso de la camioneta  vacía y el peso de la carga que lleve no debe ser inferior que 415 kg. Si hay que cargar cuatro cajones iguales, el peso máximo que puede pesar cada uno de los cajones para poderlos llevar en la camioneta es:

A.    115 kilos

B.    15 kilos

C.    100 kilos

D.    150 kilos

10.  La microempresa de buñuelos de don Jacinto cobra a sus acreedores $ 300 por cada buñuelo más un valor fijo de $ 200. La microempresa de doña Pepa que le hace la competencia a don Jacinto cobre a $ 250 buñuelo más un valor fijo de $ 300. ¿Cuántos buñuelos tiene que vender don Jacinto para obtener más dinero que la competencia?

 11. Las menos  tres quintas partes de un número disminuido en un medio es menor que los menos tres décimos del mismo número aumentado en un cuarto. El problema escrito en forma de ecuación es:

A.    - 3⁵ x – ½ ˂ - 3¹⁰ x + 4

B.    - 3/5 x – ½ ˂  - 3/10 + ¼

C.     - 3/5 x – ½  ≤ 3/10 + ¼

D.     - 3/5 x – 2  ≤ 3/10 + ¼

12. Al resolver la inecuación  2 ≤ 4x - 20  ˂ 24, se encuentra que su solución numérica, su  gráfica e intervalo es:

 13.  Multiplique las fracciones algebraicas:

v  Recordemos las propiedades de los radicales:

Sean las siguientes operaciones de suma y resta de radicales:

 14. Al resolver el literal a) su solución es:

             A.  3√12

                B.  √12

                C.  3√3

                D.  √3

             15. Al resolver la suma del literal d, su respuesta es:

                  A.  ∛2

                 B.  4∛2

                 C.  2∛4

                 D.  ∜2

16.  Resuelva la operación del literal e.

17.  Simplifique  los radicales:

a.  ∛(16 a^(4 ) ) b^6

b. √(8m^3 n^4  z^5 ) 

18.  Racionalice las siguientes fracciones:

 1).  (4√5)/√7

  2).  (∛2)/(∛128) 

 3.  (3√6)/(√7-10)

1). 

2).  

3). 

Prof. Éver Chalarca Bedoya

Taller de repaso segundo período

TALLER DE REPASO – GRADO 10,1

SEGUNDO PERÍODO 2019

11.  Según la gráfica, la figura que corresponde a una función biyectiva es:

A.     Figura 1                      

B.    Figura 2                   

C.    Figura 3                

D.    Figuras 1 y 3

2 2.  Según la gráfica del plano cartesiano, corresponde a:

                           

A.    Función inyectiva        

B.    Función sobreyectiva          

C.    Función biyectiva         

D.    Ninguna

3  3.  Indique el dominio Dm f(x) y el rango Ran f(x) de la gráfica.

                      

               

44.  .     Dada la función  x²– 1/2, determine su dominio y su rango.

55.  .     Tabule y grafique la función y =  x^2 + 3x  -4

66.       Una función se puede expresar mediante.

                        

A.    Expresión algebraica

B.    Tabla de valores

C.    Representación gráfica

D.    Todas las anteriores

7. Grafique la función f(x) = 2^x -3

8. Dada la relación R= {(x,y)  / x^2+ y^2=1}   , su gráfica corresponde a:

A.    Una línea recta                 

B.  Una parábola                 

C.  Una hipérbola          

D.  Un círculo

9. La parábola corresponde a una relación de la forma:

A.  R= {(x,y)  / x^2+ y^2=1}                        

B.  R= {(x,y)  / 2x+ y=1}

C.  R= {(x,y)  /   〖3x〗^2- y=1}

D.  R= {(x,y)  / x^2-3 y^2=1} 

         

10.  Si una rueda gira 10/4 π  rad en 4 segundos, entonces de cuántos grados es su giro.

11. Dada la figura, determine la longitud de arco S en radianes

                      

                

12. Un círculo tiene un radio de 10 pulgadas y un ángulo central AOB hace el arco AB de longitud 2 pies. Determine la medida en radianes del ángulo AOB.

13.  Expresar la medida en grados, minutos y segundos de la gráfica dada.

                          

14.  El péndulo de un reloj mide 40 cm y en su movimiento se desplaza    A cada lado vertical.  ¿Cuál es la longitud de arco que describe

15.  Las circunferencias tangentes son la vista lateral de tres rodillos. El rodillo con centro en C gira con una frecuencia de 960 rpm. Entonces su velocidad angular (  es:

  

        A. 20.000 cm/min

        B. 24.127 cm/min

        C. 27.000 cm/min

        D. 30.000 cm/min

16. 240 rpm equivalen a:

       A. 240  rad

       B. 120  rad

      C. 480  rad

      D. 600  rad

17. Determine el largo de la escalera, de acuerdo a las medidas dadas.

    

18.  Dado el triángulo

  

                                           

Determine las relaciones trigonométricas que se dan.

Prof. Éver Chalarca Bedoya