TALLER
DE REPASO – GRADO 9, 1,2
SEGUNDO
PERÍODO 2019
1. Resuelva las
siguientes expresiones algebraicas con productos notables o casos de
factorización según sea el caso:
1). (4x – 7) (4x
- 7)
2). 169m10
– 78m5 + 9
3). 9y4
– 100:
4). 25x3
+ 15x2 – 10x
5). 3abx2
– 2y2 – 2x2 + 3aby2
6). x2
– 2x - 120
2. Al
resolver la inecuación – 12x + 15 ≥ -
13 – 2x, el valor de la x es:
A.
x
≥ 5
B.
x
≤ 1/5
C.
x
≥ 1/5
D.
x
≤ - 1/5
3. Expresa
la solución a la inecuación anterior por intervalo y por comprensión
4.
Dada la gráfica, exprese la solución por intervalo y por comprensión
5. Dado el conjunto por comprensión: A= : A= {x /x ∈R,-5≤x ≤ 1}
,
su representación por intervalo es:
v Sean las gráficas:.
6. El
intervalo ] ∞, 3 ] representa la
solución de:
A.
La
figura 1
B.
La
figura 2
C.
La
figura 3
D.
La
figura 4
7. El
intervalo ]5, ∞ [ representa la solución de:
A.
La
figura 1
B.
La
figura 2
C.
La
figura 3
D.
Ninguna
de las anteriores
8.
Exprese la solución numérica y por comprensión de cada una de las figuras o
gráficas dadas.
v Dados los problemas, plantee
una solución y resuélvalos
9. Una camioneta pesa 875 kg. La diferencia entre el peso de la camioneta
vacía y el peso de la carga que lleve no debe ser inferior que
415 kg. Si hay que cargar cuatro cajones iguales, el peso máximo que puede pesar cada uno de los
cajones para poderlos llevar en la camioneta es:
A.
115
kilos
B.
15
kilos
C.
100
kilos
D.
150
kilos
10. La microempresa de buñuelos de don Jacinto
cobra a sus acreedores $ 300 por cada buñuelo más un valor fijo de $ 200. La microempresa
de doña Pepa que le hace la competencia a don Jacinto cobre a $ 250 buñuelo más un valor fijo
de $ 300. ¿Cuántos buñuelos tiene que vender don Jacinto para obtener más dinero que la
competencia?
A.
-
35 x – ½ ˂ - 310 x + 4
B.
-
3/5 x – ½ ˂ - 3/10 + ¼
C.
- 3/5 x – ½
≤ 3/10 + ¼
D.
- 3/5 x – 2
≤ 3/10 + ¼
12. Al
resolver la inecuación 2 ≤ 4x - 20 ˂ 24,
se encuentra que su solución numérica, su
gráfica e intervalo es:
v Recordemos las propiedades de
los radicales:
Sean las siguientes operaciones de
suma y resta de radicales:
A. 3√12
B. √12
C. 3√3
D.
√3
15. Al
resolver la suma del literal d, su respuesta es:
A. ∛2
B. 4∛2
C. 2∛4
D. ∜2
16.
Resuelva la operación del literal e.
17.
Simplifique los radicales:
a.
b. √(8m^3 n^4 z^5 )
18.
Racionalice las siguientes fracciones:
1). (4√5)/√7
2). (∛2)/(∛128)
3. (3√6)/(√7-10)
1).
2).
3).
Prof. Éver Chalarca Bedoya

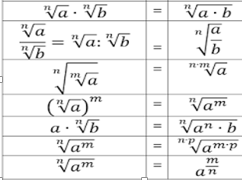

Muchas gracias profesor.
ResponderEliminargracias profe
ResponderEliminarMuchas gracias profesor
ResponderEliminarValentina gil 9-2
Muchas gracias profesor
ResponderEliminarValentina gil 9-2
Muchas gracias profe
ResponderEliminarAtt:José David Jiménez c,Lorena madrid berrio y paola Teherán 9.2
Muchas gracias profe Ever
ResponderEliminarMuchas gracias profe
ResponderEliminarSantiago moreno 9-2